ইতিহাস লেখার রাজনীতি ও ভারতীয় গণিতের ইতিহাস

-শ্রী অশেষ উপাধ্যায়

আধুনিক ভারতে ইতিহাস চর্চায় বাঙ্গালী বিজ্ঞান চর্চার মতই ছিল পুরোধা। কি ইতিহাস চর্চার অগ্রদূত যদুনাথ সরকার, কি জাতীয়তাবাদী সত্যদ্রষ্টা রমেশ চন্দ্র মজুমদার, কি বামপন্থী সুশোভন সরকার, আধুনিক ভারতে ইতিহাস চর্চার যুদ্ধক্ষেত্রে যুযুধান দুই পক্ষেরই সেনাপতিরা বেশিরভাগই ছিলেন বাঙ্গালী। ভারতীয় আধুনিকতার জন্মভূমি এই বঙ্গদেশ আধুনিকতার দুই স্তম্ভ বিজ্ঞানচেতনা ও ইতিহাস চেতনা এই দুই ক্ষেত্রেই পুরোধা হওয়ায় ভারতের রাজনৈতিক অন্তরাত্মা দখলের যে লড়াই জাতীয়তাবাদীদের ও আব্রাহামিকদের মধ্যে যে চলছে তারও সূচনা হয় বাঙ্গালীদের কাজের সূত্র ধরেই। যদুনাথ সরকারের কাজ যে বামপন্থী ও ইসলামিকদের সমবেত নোংরামির শিকার হয়, রমেশ চন্দ্র মজুমদারকে কিভাবে স্বাধীন ভারতে কংগ্রেসি সরকারের দ্বারা হেনস্থা হতে হয় তা আজ সকলের জানা। উভয় ক্ষেত্রেই সংঘাতের মূল কারণ ছিল সত্যনিষ্ঠ ভাবে এমন ইতিহাস লেখা যা ভারতে নিজের সাংস্কৃতিক শিকড়ের ব্যাপারে সচেতন ও আত্মবিশ্বাসী হতে সাহায্য করবে। যা কিনা আব্রাহামিকদের বৃহত্তর স্বার্থের চরম পরিপন্থী।

 আব্রাহামিকদের হিংস্রতা সম্ভবত প্রাচীন ভারতের বিজ্ঞান চর্চার ইতিহাসের ক্ষেত্রে যতটা তীব্র হয় তা অন্য কোন ক্ষেত্রে হয় না। এই বিষয়ে কমিউনিস্ট, সোশালিস্ট, পাশাত্য জাতীয়তাবাদী, ইসলামিক, খ্রিস্টান, আব্রাহামিক এথিইস্ট সবাই এক কাট্টা ভারতীয় সভ্যতার অবদানকে আজকের ভারতীয়দের কাছে অজানা করে রাখতে। আসলে এ লড়াই শুধু জাতীয় গৌরবের লড়াই নয়। সমস্যাটা আরও গভীরে। আধুনিক সভ্যতাকে আব্রাহামিকরা ইউরোপীয় এনলাইটমেনট এর ফল মনে করে। এক ইসলামিসটরা বাদে উপরিউক্ত সবাই সে বিষয়ে একমত। বিজ্ঞান চিন্তায় গণিতের প্রয়োগ হচ্ছে এই সভ্যতার সবথেকে শ্রেষ্ঠ কীর্তি, এনাদের মতে। এবং এটা এসেছে গ্রীক দর্শন ও খ্রিস্টান আধ্যাত্মিকতার উত্তরসূরি হিসেবে।আজকের scientific rationalism এনাদের মতে গ্রীক ও খ্রিস্টান rationalism এর আধুনিকতম রূপ। ইস্লামিসটরাও একমত তবে এর সাথে ইসলামি সভ্যতার অবদানটা জুড়ে দিতে চান।কিন্তু মূল প্রতিপাদ্য নিয়ে তাদের কোন আপত্তি  নেই কারণ খ্রিস্টানদের  মতই ইসলামও rationalism নিয়েছে গ্রীস থেকেই। এই যুক্তির সূত্র ধরে আসে অকথিত আব্রাহামিক দাবী যে আধুনিক বিশ্বের একমাত্র চিন্তন পদ্ধতি হবে আব্রাহামিক। আজ যে সনাতন ভারতীয় সংস্কৃতির বিরুদ্ধে “Marxist-Islamist-Christian” alliance এর সাম্রাজ্যবাদের বিরুদ্ধে জাতীয়তাবাদীরা সরব সেই সাম্র্যাজ্যবাদের শিকড়ে আছে ওপরে বর্ণনা করা এই বৌদ্ধিক সাম্রাজ্যবাদ।

ভারতীয় বিজ্ঞানের ইতিহাস এই বৌদ্ধিক সাম্রাজ্যবাদের পথে সবচেয়ে বড় বাধা। কারণ ভারতের সিদ্ধান্ত ধারার গণিত জ্যোতিষ। জ্যোতির্বিদ্যার চর্চায় ভারতে শুধু সফলভাবে গণিতের ব্যাবহারই হয়নি, প্রয়োজনে গবেষণার মাধ্যমে গণিতকে উন্নততর করা হয়েছে। দশমিক পধতি, শূন্য ও ঋণাত্মক সংখ্যা সম্বলিত পাটীগণিত যা ভারতের অনবদ্য অবদান, তা সভ্যতার ইতিহহাসের প্রথম algorithm গুলোর জন্ম দিয়েছে। ভাগ পদ্ধতি, বর্গমূল ও ঘনমূল পদ্ধতির এরই নিদর্শন। প্রাথমিকে শেখা এই মূল্যবান জিনিসগুলির মুল্য এক মুহূর্তে পরিষ্কার হবে যদি রোমান সংখ্যা পদ্ধতি নিয়ে গুন ভাগ করতে জান। জ্যামিতিতে উৎকর্ষের শ্রেষ্ঠে ওঠা গ্রীকরা এই দশমিক পদ্ধতি না জানার ফলে কোনদিন পাটীগণিত টপকে বীজগণিতে পৌছতে পারেনি। অন্যদিকে ভারতীয় পাটীগণিত ও জ্যামিতিতে ছিল sophisticated algorithms এর ছড়াছড়ি। আসলে ভারতীয় পাটীগণিত, জ্যামিতি এমনকি পাণিনীয় ব্যাকরণের মূল্য ভাবই ছিল বীজগাণিতিক। এই বীজগণিত পূর্ণ মাত্রায় স্বতন্ত্র বিষয় হয়ে ওঠে Aryabhatta, Brahmagupta আর Bhasrcaracharya এই ত্রয়ীর হাত ধরে। এমনকি আধুনিক বীজগণিতের জন্মও বলা যায় Brahmaguptaর হাতেই। শুধু তাত্ত্বিক ক্ষেত্রেই না জ্যোতির্বিদ্যার অবশ্যম্ভাবী আনুষঙ্গ হিসেবে সূর্যঘড়ি ও অন্যান্য জ্যোতির্বিদ্যার যন্ত্রপাতি তৈরিতেও উৎকর্ষ দেখা যায়।তাই আধুনিক বিজ্ঞানের সবকটি উপাদানী ছিল এই ধারায়। এই ইতিহাস আধুনিকতার ওপর পাশ্চাত্যের একচেটিয়া দাবীকে শুধু প্রশ্নের মুখে ফেলে না western rationalism এর একমাত্র rationalism হবার দাবীকেও নস্যাৎ করে।

আধুনিক যুগে ভারতের এই সত্যকে খুঁজে আনতে অনেকেই ব্রতী হয়েছিলেন। ইতিহাসের অন্যান্য ক্ষেত্রের মত এখানেও পুরোধাদের একজন ছিলেন এক বাঙ্গালী, বিভূতিভূষণ দত্ত বা স্বামী বিদ্যারন্য। তাঁর অনবদ্য কীর্তি Awadesh Narawan Singh এর সাথে যৌথ ভাবে লেখা History of Hindu Mathematics: A Source Book. এই বইটি ভারতীয় গণিতের ইতিহাসে যদুনাথ সরকারের মুঘল আমলের ইতিহাসের সাথে তুলনীয় ব্যাপ্তি ও গভীরতায়। এই বইটি ভারতীয় গণিতের ইতিহাসের গবেষণায় এক অমূল্য দলিলই শুধু নয় আব্রাহামিকদের বিরুদ্ধে লড়াইয়ে এক ব্রহ্মাস্ত্র। দুর্ভাগ্য বশত ১% মানুষও এনার বা এনার বইটির কথা জানেন কিনা জানি না। ঠিক যেমন ভারতীয় গণিতের মহামূল্য অবদানগুলিও বেশির ভাগ মানুষের অজানা।

কয়েকটি সহজ উদাহরণ দিয়ে পাঠকে ভারতীয় গণিতের মূল সুরটি বোঝাবার চেষ্টা করি। মহর্ষি পিঙ্গলের ছন্দ শাস্ত্রের নাম অনেকেই শুনেছেন কিন্তু জানেন কি এটিকে combinatorics এরও treatise হিসেবে ধরা হয়? এতে 2^n বার করার algorithm, binomial coefficients কাজ, binary numbers ইত্যাদির ওপর কাজ আছে। ছন্দশাস্ত্রে মাত্রার ওপর কাজ করতে গিয়ে Virahanka ৬০০ খ্রিস্টাব্দের কাছাকাছি তথাকথিত Fibonacci Numbers আবিষ্কার করেন। ওনার কাজ ছিল এরকমঃ ছন্দ দুরকমের হয়, লঘু ও গুরু। একটি ছন্দবাক্য হল পরপর কয়েকটি ছন্দের সমষ্টি। যেমন “লঘু গুরু লঘু লঘু” একটি ৪ দৈর্ঘ্যের ছন্দবাক্য। সঙ্গীতে “রে নি রে রে ” এই সুরটি এই ছন্দ্যবাক্যের আওতায় পড়ে। তেমনি “ধা নি নি গা রে” সুরটি আসে “গুরু গুরু গুরু লঘু লঘু” ছন্দ্যবাক্যের আওতায়।

Virahanka সঙ্গীতের অন্তর্নিহিত গণিত কে নিয়ে চিন্তা করছিলেন। এখন একটা সমস্যা নিয়ে উনি চিন্তা করছিলেন যে যে কোন সংখ্যা n এর জন্য n মাত্রার কতরকম ছন্দবাক্য আছে। উনি সমস্যাটিকে এইভাবে সমাধান করেনঃ ধরে নি লঘু ছন্দের মান ১ আর গুরুর ২। একটি ছন্দবাক্যের মান তার সব ছন্দের মানের যোগফল। Virahanka দেখেন যে n-1 মাত্রার যে কোন ছন্দবাক্যের শেষে একটা লঘু বসালে বা n-2 মাত্রার যে কোন ছন্দবাক্যের শেষে একটা গুরু বসালে আমরা n মাত্রার ছন্দবাক্য পাই। যেমন “রে নি রে রে ” হল “লঘু গুরু লঘু লঘু” ধরনের ছন্দবাক্য। এর মান ৫। এর শেষে রে বা গা ইত্যাদি বসালে “লঘু গুরু লঘু লঘু লঘু ” তৈরি হয় যার মান ৬। আবার ধা বা নি বসালে “লঘু গুরু লঘু লঘু গুরু” তৈরি হয় যার মান ৭।

আবার n মাত্রার ছন্দবাক্যের শেষ ছন্দটি মুছে দিলে একটা n-1 বা n-2 মাত্রার ছন্দবাক্য পাই শেষ ছন্দটি যথাক্রমে লঘু বা গুরু হলে। যেমন “রে নি রে রে ” এর শেষ ছন্দ রে কে মুছে দিলে পাই “রে নি রে” যা কিনা “লঘু গুরু লঘু” ছন্দবাক্য এবং এর মান ৪, যা হল ৫-১। তেমনি “রে রে নি” র মানও ৪ আর এর শেষ ছন্দ নি, যা কিনা গুরু ছন্দ, তাকে মুছে দিলে পাই “রে রে” যার মান ২, যা হল ৪-২।

এখন n মাত্রার সব ছন্দবাক্যের সংখ্যা f(n) হলে ওপরের আলোচনা থেকে আমরা পাই f(n)=f(n-1)+f(n-2). একমাত্রার একটিই ছন্দবাক্যঃ শুধু একটি লঘু ছন্দ তাই f(1)=1. দুই মাত্রার দুটি ছন্দবাক্যঃ দুটি লঘু বা একটি গুরু তাই f(2)=2. এখন ওপরের ফরমুলা থেকে আমরা পাই f(3)=1+2=3, f(4)=2+3=5, f(5)=5+3=8 …..এই ভাবে আমরা যে রাশিটি পাই তা হল {1,2,3,5,8,13,21,34…..} যা কিনা Fibonacci রাশি নামে পরিচিত। সালটা লক্ষ্য করুন পাঠক, ৬০০ খ্রিস্টাব্দের কাছে, মানে ফিবনাচ্চির প্রায় ৬০০ বছর আগে!

আরেকটি উদাহরণ দিঃ অনেকেই শুনেছেন Boudhayan এর সুল্ব সূত্রে তথাকথিত পিথাগোরাস এর উপপাদ্য আছে। এটা বলেই একটু শিক্ষিত দেশই বিদেশি আব্রাহামিক মাত্রেই (কাকেশ্বর কুচকুচের মত) বলবে থাকলেও নাকি ওই উপপাদ্যের প্রমাণটা ছিল না। অথচ পিথাগোরাস উপপাদ্যের যে মূল সম্পাদ্য বা construction টা, মানে সমবাহু ত্রিভুজের লম্ব ও ভূমির ওপর দুটো বর্গক্ষেত্র দেয়া থাকলে অতিভুজের ওপর বর্গক্ষেত্র টা কিভাবে আকা যায়তা ধাপে ধাপে বর্ণনা করা আছে। শুধু তাই না দুটি সংখ্যা a, b দেয়া থাকলে কিভাবে জ্যামিতিক ভাবে ab এর বর্গমূল বার করা যায় তা এই ভাবে বলা আছেঃ
১। ধরে নিই a হতে b ছোট
২। a ও b মাপের বাহুর আয়তক্ষেত্র নেয়া হোক
৩। a মাপের বাহুর অপর থেকে b মাপের অংশ কাটা হোক।
8। বাকি অংশটিকে দ্বিখণ্ডিত করা হোক (পাঠক দেখুন: এই দ্বিখণ্ডিত দুই অংশের প্রটেকতি (a-b)/2)
৫। a মাপের বাহুর ওপর b মাপের অংশ এবং তাঁর সংলগ্ন দ্বিখণ্ডিত অংশের একাংশ কে মিলিয়ে যে রেখাংশ তাকে ব্যাসার্ধ করে দ্বিখনডন বিন্দুকে কেন্দ্র করে বৃত্তচাপ আকা হক। (পাঠক দেখুন: এর ব্যাসার্ধ b + (a-b)/2 = (a+b)/2.)
৬। এবার a মাপের বাহুর ওপর b মাপের রেখাংশ যেখানে সেস হয়েছে সেখানে লম্ব অঙ্কন করুন। সেই লম্ব আগের ধাপে আকা বৃত্তচাপ কে যে বিন্দুতে ছেদ করে সেই পর্যন্ত রেখাংশের দৈর্ঘ্য a.b র বর্গমূল।(পাঠক দেখুন: এটা হচ্ছে ab= ((a+b)^2 – (a-b)^2)/4 বলে।

নিচের ছবিতে এই পদ্ধতিটি ব্যাখ্যা করা হয়েছে:

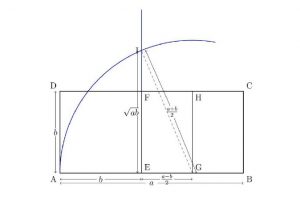
যেখানে এরকম detailed algorithm দেয়া আছে সেখানে বাকি কি থাকে? আসলে গণিতে “প্রমাণ” বলতে আমরা axiomatically presented deductive reasoning বুঝি যেটা নিঃসন্দেহে গ্রীকদের অসামান্য অবদান কিন্তু সেটাই কিন্তু একমাত্র approach নয় গণিতে। গ্রীকরা গণিত কে যুক্তিবিদ্যার অংশ হিসেবে দেখেছে যেখানে ভারতীয়রা দেখেছে বীজগাণিতিক বিজ্ঞান হিসেবে। ভারতীয় গণিতকে বুঝতে গেলে তার নিজের methodology কে বুঝতে হবে। আর এই methodology কে বোঝাই কিন্তু ভারতাত্মার শিকড়কে সন্ধান, প্রকৃত ভারতীয় জীবনবোধকে খুঁজে বার করা।

এটাই আব্রাহামিক সাম্রাজ্যবাদের সবথেকে বড় দুঃস্বপ্ন, মনেপ্রাণে ভারতীয় ভারতবর্ষ। তাই ভারতীয়দের ভারতীয় গণিত ও বিজ্ঞানের ইতিহাস সাধনা থেকে বিরত করতে সর্বশক্তি দিয়ে ঝাঁপায় তারা।

(লেখক পরিচিতি: গড়িয়া নিবাসী বঙ্গভাষী ভারতীয়। পেশা শিক্ষকতা ও লেখালেখির চেষ্টা করা)

কাঞ্জিক কৃষ্টি